A 4 minutes story written on Oct 2017 by Adrian B.G.

Writing O(1) high performance data structures is a multi-post series:

1. Hierarchical Queue
2. Hierarchical Heap (this article)
3. Ladder Queue (soon)> A priority queue is an abstract data structure, used to store values (any data) with a priority. You can insert data at any time with any priority, but you can only take out the value with the highest priority.

When to use priority queues ⁉

I confess, I didn’t use many of them in my apps, but there are a few problems perfect for it:

• triage — any processing you have based on a score/importance
• ordering — when your data has a specific order of processing/analysis, ex: process the DAU KPI before MAU
• Event driven simulation — priorities can be timestamps
• Graph searching
• Load balancing — the priority is the inverse of the load

Hierarchical Heap 🔬

The Hierarchical Heap is a (very) fast priority queue, it can be used with a large dataset and it has a big priority cardinality.

I could’t find an open source implementation of this algorithm, so I don’t have a comparison term, the structure doesn’t even have a wiki page.

From my knowledge this data structure was proposed by Cris L. Luengo Hendriks in “ Revisiting Priority Queues for Image Analysis”.

The Hierarchical Heap is a newer version of the [Hierarchical Queue] (https://coder.today/fast-priority-queues-in-go-hierarchical-queue-86daf6a7553a)structure, it removes the limitations by adding some complexity (O(log n/k) compared to (O(1)). HH is similar to the SplayQ(ueue) structure.

The HQ has 1 bucket for each priority value, instead HH is grouping more distinct values into one bucket, having K ≤ N buckets.

“By dividing the N elements in the queue over k buckets, the average size of each heap is reduced by a factor k, and the enqueueing and dequeueing operations thus are of order O(logN/k) if the buckets are chosen correctly.”

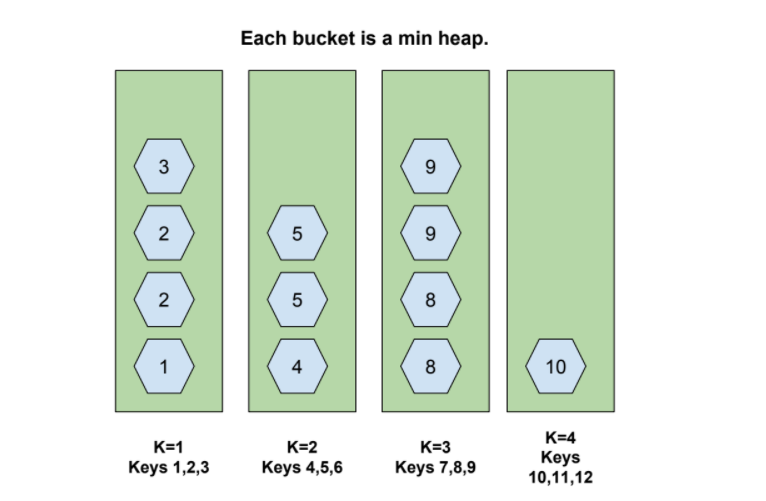
Each bucket is in charge of sorting its containing values, by keeping a low cardinality of priority values per bucket this operation will be seamless.

Using the following function you can find out in which bucket a specific priority value should be enqueued:

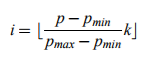
where K is the number of buckets, and pMin/pMax are the minimum and maximum priority values allowed for this HH instance.

The dequeue operation is simple too, you must find the lowest non empty bucket and extract the next priority (pop from a Min Heap).

Go code go ✏

The keys are of typeint and the highest priority is 0. Each bucket is a Min Implicit Heap (a sorted list of priorities, more exactly a special version of a binary tree, stored in an array) and values can be anything:interface{}.

With the right bucket/priority diversity it can approach the HQ performance by a factor of 0.5.

For the best performance benchmark the Enqueue/Dequeue functions with your own data, and tweak the parameters (buckets,minP,maxP) until you get the maximum performance.

If K is too small (relative to N, max priority), the buckets will contain too many distinct priority values, and the performance will decrease. Theoretically the K=1 is the fastest way (it is identical with Hierarchical Queue), but it will consume more memory, each bucket adding its overhead.

The buckets can be reused, so you can keep adding new priorities at the same time as you are retrieving them.

By applying the robustness principle we allow any priority value to be added in the queue. It simply adds the new value to the first or last bucket if it exceeds the min or max values.

Because concurrency is important in Go, the structure has a mutex. It can be used manually or automatically (each function call blocks the mutex).

The bucket size is dynamic, the size of the slices (array) has a minimum value of 8 elements and doubles each time it is filled, and shrinks by half each time N < size/4. You can inspect the Heap code here: bgadrian/data-structures

Packing up 🗃

The Hierarchical Heap data structure is part of “bgadrian/data-structures/priorityqueue” Go package. It has 100% test coverage, examples, benchmarks and documentation.